Diferencia entre revisiones de «Modelo de datos»
De iMMAP-Colombia Wiki
(Página creada con «Un modelo de datos en SIG es una construcción matemática para representar objetos geográficos o superficies como datos. Así, estos permiten que un computador repres…») |
|||
| Línea 38: | Línea 38: | ||
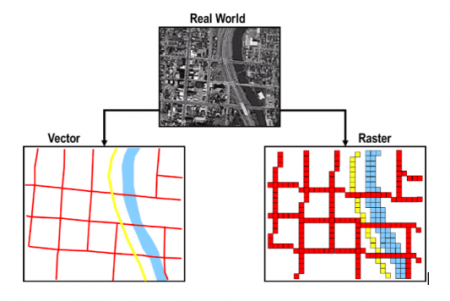
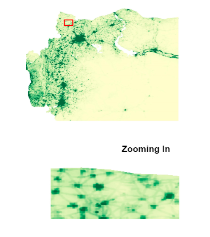
La noción de representación ráster se basa en una organización celular que divide el espacio en una serie de unidades en donde cada unidad es generalmente de tamaño similar a la otra. Así, las características de los datos se dividen en matrices celulares y se asigna una coordenada (X, Y) a cada celda y un determinado valor. Las celdas de cuadrícula son la representación ráster más común. Un ejemplo del modelo ráster son las imágenes satelitales. | La noción de representación ráster se basa en una organización celular que divide el espacio en una serie de unidades en donde cada unidad es generalmente de tamaño similar a la otra. Así, las características de los datos se dividen en matrices celulares y se asigna una coordenada (X, Y) a cada celda y un determinado valor. Las celdas de cuadrícula son la representación ráster más común. Un ejemplo del modelo ráster son las imágenes satelitales. | ||
| − | [[Archivo:Modelo Ráster.png| | + | [[Archivo:Modelo Ráster.png|700px|sinmarco]] |
Traducir un modelo ráster al mundo real implica: | Traducir un modelo ráster al mundo real implica: | ||
Revisión del 13:04 20 nov 2020
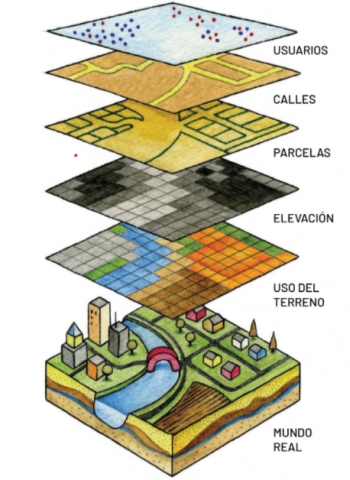
Un modelo de datos en SIG es una construcción matemática para representar objetos geográficos o superficies como datos. Así, estos permiten que un computador represente elementos geográficos reales como elementos gráficos. En el momento predominan dos modelos de representación; ráster (basado en cuadrículas) y vector (basado en líneas).
Sumario
Modelo Vectorial
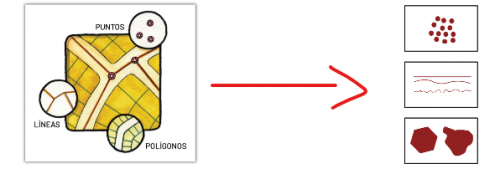
¿Qué es un vector?
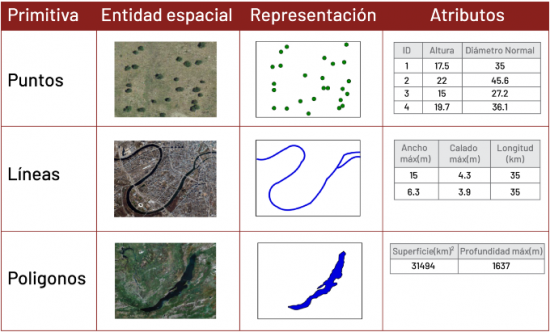
El concepto de datos vectoriales asume que el espacio es continuo, en lugar de fragmentado, lo que da un conjunto infinito (en teoría) de coordenadas. Una representación vectorial se compone de tres elementos principales: puntos, líneas y polígonos.
Los puntos son objetos de dimensión cero que contienen solo un par de coordenadas estos representan, por ejemplo, la ubicación de un dispositivo móvil, de una estación meteorológica, de un supermercado, etc. Las líneas son entidades unidimensionales compuestas de múltiples puntos conectados, entre sus representaciones se encuentran una calle, un río, el seguimiento desde un dispositivo, etc. Los polígonos son entidades bidimensionales creadas por múltiples líneas que se repiten para crear una entidad "cerrada“, por ejemplo, los límites del país, lagos, edificios, entre otros.
Ejemplo de un modelo de representación vectorial con cada uno de sus elementos y atributos asociados:
Ventajas y Desventajas
El modelo vectorial tiene tanto puntos a favor como en contra en el momento de realizar la representación de los datos.
Ventajas:
- Mejor representación de la realidad (exactitud y precisión).
- Al alterar la escala de observación, la vista no cambiará incluso si se acerca mucho.
- Estructura de datos compacta (los archivos vectoriales son mucho más pequeños que los ráster).
Desventajas:
- Estructura de datos compleja.
- Implementación complicada del análisis espacial.
- Difícil de manipular.
- Es posible que se requiera un software especial para abrir datos vectoriales.
Modelo Ráster
¿Qué es una representación ráster?
La noción de representación ráster se basa en una organización celular que divide el espacio en una serie de unidades en donde cada unidad es generalmente de tamaño similar a la otra. Así, las características de los datos se dividen en matrices celulares y se asigna una coordenada (X, Y) a cada celda y un determinado valor. Las celdas de cuadrícula son la representación ráster más común. Un ejemplo del modelo ráster son las imágenes satelitales.
Traducir un modelo ráster al mundo real implica:
- Tener una representación de la realidad.
- Vinculación de atributos a la representación.
- Crear relaciones espaciales entre representaciones.
Ventajas y Desventajas
El modelo ráster tiene tanto pros como contras al momento de realizar la representación de los datos.
Ventajas:
- Estructura de datos simple.
- Superposición fácil.
- Tamaño y forma uniformes.
Desventajas:
- Gran cantidad de datos.
- Diferentes escalas entre capas pueden ser un poco difícil de manejar.
- Se puede perder información debido a la generalización.
Ejemplo
Para lograr un sistema de coordenadas del mundo real es necesario primero realizar una representación de la realidad, luego vincular los atributos de dicha representación y, por último, crear relaciones espaciales entre las representaciones.