Limitaciones a los datos
De iMMAP-Colombia Wiki
En la actualidad los datos y su manejo estadístico son uno de los principales paradigmas para la toma de decisiones. Los datos nos permiten reducir un panorama extremadamente complejo a uno mucho más simplificado para lograr una respuesta humanitaria eficiente.
No obstante, debemos tener en cuenta que existen ciertas limitaciones a la hora de manejarlos que pueden dificultar la toma estratégica de decisiones, dichas limitaciones se refieren principalmente a la configuración de un sesgo estadístico que arrojará datos que no representarán adecuadamente la población, dificultando la labor humanitaria; tomar decisiones con base en información incorrecta, lleva a ineficiente uso de los recursos, subestimar o realizar algún daño.
Sumario
Estadística Inferencial
Para contrarrestar las limitaciones, se hace uso de la estadística inferencial, la cual es la rama de la estadística encargada de hacer deducciones, es decir, inferir propiedades, conclusiones y tendencias, a partir de una muestra del conjunto. Su objetivo principal es interpretar, hacer proyecciones y comparaciones.
Ventajas
El uso de la estadística inferencial es de gran utilidad cuando:
- Se tienen datos parciales y se requiere saber una conclusión general, por ejemplo, cuando tenemos una pequeña muestra de datos sobre unos municipios y necesitamos proyectarlos para todo el departamento.
- Se necesita tomar decisiones que impactan a individuos no observados, como nuevos refugiados, migrantes, víctimas, organizaciones, etc.
- La población de estudio es amplia y resulta costoso o difícil realizar una observación completa.
- Se requiere información confiable de forma rápida.
Desventajas
Aún cuando la estadística inferencial es de ayuda, no siempre se puede utilizar. Para lograr una correcta inferencia estadística es fundamental que los datos sean seleccionados de manera aleatoria, es decir, que se pueda obtener información de distintos tipos de personas de la población objeto de estudio de la forma más amplia posible, asegurando que cada sector, tipo de característica, estén representados en los datos. De lo contrario, seleccionando una muestra con características específicas, al proyectar a la globalidad se corre el riesgo de que no se capture la información correcta de la población objeto, creando un sesgo.
Un ejemplo es cuando, con el objetivo de caracterizar a una población migrante, se recolecta información solo de los beneficiarios de un programa, como podría ser mujeres cabezas de hogar con dos hijos, y a partir de allí se generaliza que la mayoría de la población migrante son madres solteras.
Formas de evitar el sesgo
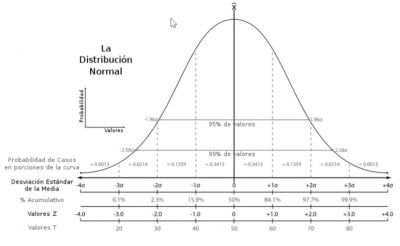
Existen diversas estrategias estadísticas para evitar que ocurra el sesgo. Una de estas es el Teorema del límite central, el cual indica que al tomar, promediar y graficar Y cantidad de muestras de una población X, se obtiene una distribución normal, es decir, mediante la distribución de los distintos promedios se logran unos datos que representan el comportamiento de todo el grupo.
De esta manera, el teorema indica que cuando obtenemos un promedio de una muestra de forma aleatoria, este promedio tiende por lo general, bajo condiciones normales, a estar cercano al promedio de la toda la población en sí, es decir, a su realidad. Entonces el principal método para evitar el sesgo es realizar una captura de información donde cada punto de la población esté representado y donde todos tengan la misma probabilidad de ser seleccionados. Así mismo, otro aspecto importante es que el comportamiento normal promediado se obtenga de al menos 30 muestras, independientemente del número total de la población.
Como ejemplo, tomemos la imagen de arriba. En primer lugar se puede observar el territorio objeto de estudio, un asentamiento anormal de migrantes en el que pueden vivir cerca de 1000 personas. En la segunda imagen se están encuestando solo dos puntos, cada punto con dos observaciones, es decir que se toma una muestra total de 4 encuestas. El problema es, por un lado, que la muestra no cumple el mínimo requerido de 30 observaciones y, por el otro, que al ser puntos vecinos no sea un dato representativo y aleatorio de toda la población, resultando en un sesgo al momento de realizar la inferencia o generalización. Por el contrario, en la tercera imagen se realizan encuestas en 16 puntos de manera aleatoria a lo largo de todo el asentamiento, es decir que se toman 32 observaciones a lo largo de todo el asentamiento, lo que fácilmente nos permitirá realizar la inferencia estadística y obtener una distribución normal que represente al total de población.